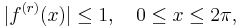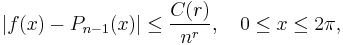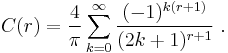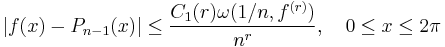Jackson's inequality
In approximation theory, Jackson's inequality is an inequality bounding the value of function's best approximation by algebraic or trigonometric polynomials in terms of the modulus of continuity of its derivatives.[1][2] Informally speaking, the smoother the function is, the better it can be approximated by polynomials.
Contents |
Statement: trigonometric polynomials
For trigonometric polynomials, the following was proved by Dunham Jackson:
Theorem 1: If ƒ: [0, 2π] → C is an r times differentiable periodic function such that
then, for every natural n, there exists a trigonometric polynomial Pn−1 of degree at most n − 1 such that
where C(r) depends only on r.
The Akhiezer–Krein–Favard theorem gives the sharp value of C(r) (called the Akhiezer–Krein–Favard constant):
Jackson also proved the following generalisation of Theorem 1:
Theorem 2: Denote by ω(δ, ƒ(r)) the modulus of continuity of the rth derivative of ƒ. Then one can find Pn−1 such that
Further remarks
Generalisations and extensions are called Jackson-type theorems. A converse to Jackson's inequality is given by Bernstein's theorem. See also constructive function theory.
References
- ^ Achieser, N.I. (1956). Theory of Approximation. New York: Frederick Ungar Publishing Co.
- ^ Weisstein, Eric W., "Jackson's Theorem" from MathWorld.
External links
- Jackson inequality on Encyclopaedia of Mathematics.